[ 알고리즘 연습 ] 2747. 피보나치 수 _ JAVA

문제

 

 

 

 

 

풀이

 

 

이 풀이법은 「 JAVA 프로그래밍 면접 이렇게 준비한다 」 책을 통해 알게 되었습니다.

 

 

참고 자료 

https://book.naver.com/bookdb/book_detail.nhn?bid=8655189

JAVA 프로그래밍 면접 이렇게 준비한다

 

 

 

너무나 유명한 피보나치의 수 문제입니다.

F(n) = F(n-1) + F(n-2)를 만족하는 피보나치 수에서 n 번째의 피보나치 수를 찾으면 되는 문제입니다.

 

저는 재귀를 이용하여 피보나치를 구현하였습니다.

 

 

 

코드가 정말 간단합니다. 하지만 이 코드는 0 ~ 45인 n의 범위에서 시간초과를 발생시킵니다.

중복된 재귀함수를 너무 많이 호출해서 발생하는 문제인데요

 

그래서 이런 경우에 중복된 함수 호출을 막기 위해 메모이제이션(memoization)이 필요합니다.

참고한 도서에서는 Map 자료구조를 이용하여 메모이제이션을 해주었습니다.

 

코드는 다음과 같습니다.

 

 

 

 

 

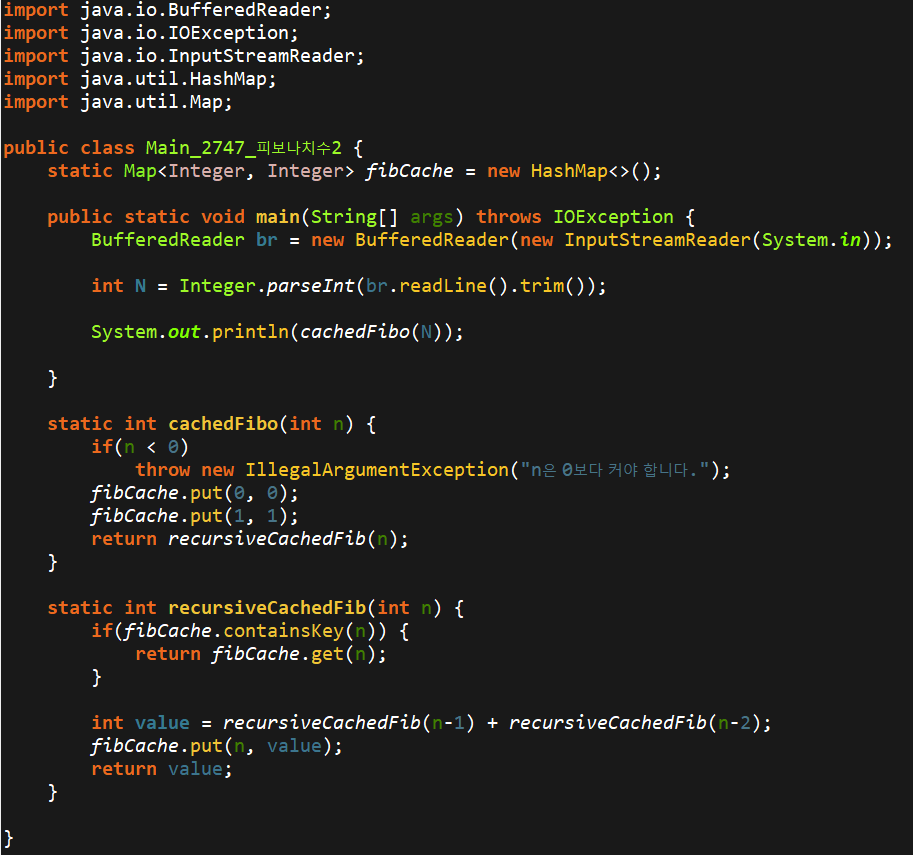
재귀함수가 중복호출되는 경우를 막기 위해 Map 자료구조를 이용해

이전에 연산한 값의 경우는 저장해놓은 값을 불러 사용합니다.

 

n이 45일 경우 어느 정도의 시간 차이가 발생할까요?

System 함수를 이용하여 연산 수행속도를 비교해보았습니다.

 

 

메모이제이션을 하지 않았을 경우 약 10초

 

 

메모이제이션을 했을 경우 0.00045초

 

메모이제이션을 한 결과

10초 -> 0.00045초로 줄어들었습니다. 메모이제이션을 해야 할 이유를 충분히 느끼실 수 있겠죠?

 

 

효율적인 문제 풀이를 위해 포스팅 해두었습니다!

 

 

 

 

출처

 

https://www.acmicpc.net/problem/2747

2747번: 피보나치 수