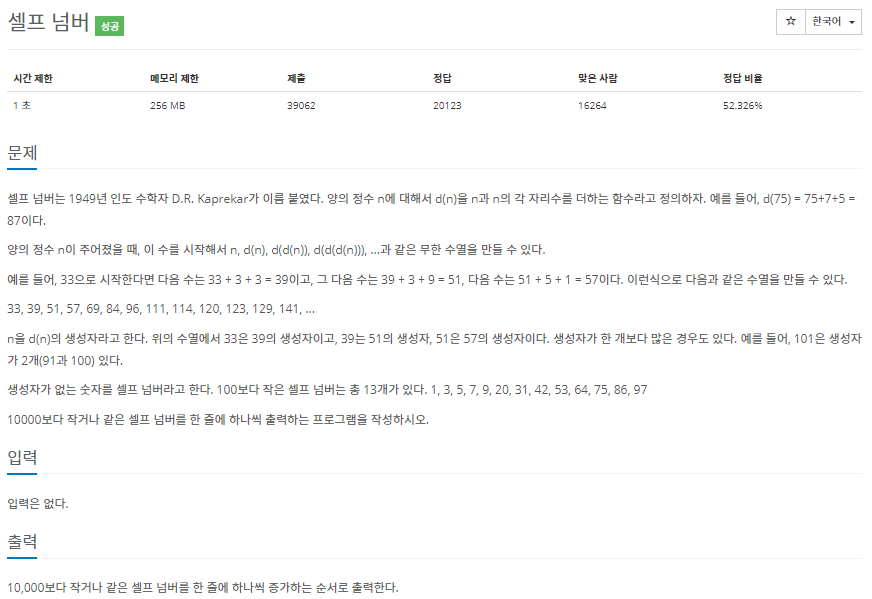
문제
풀이
이 문제를 풀이하기 전에
에라토스테네스의 체에 대해 알고 있다면 풀이에 도움이 될 것 같아 관련 자료를 찾아보았습니다.
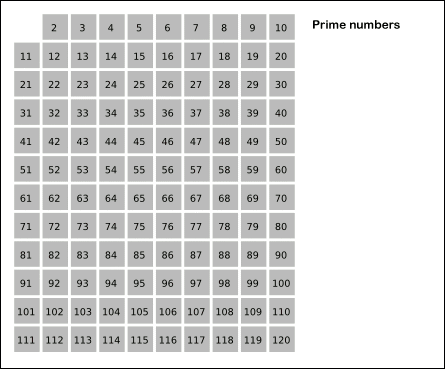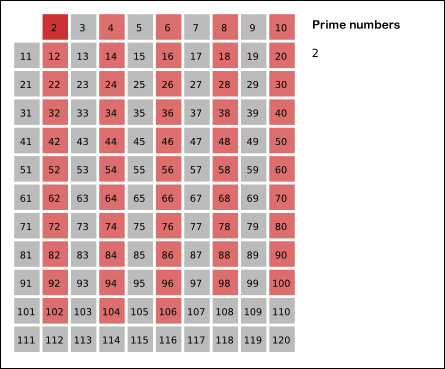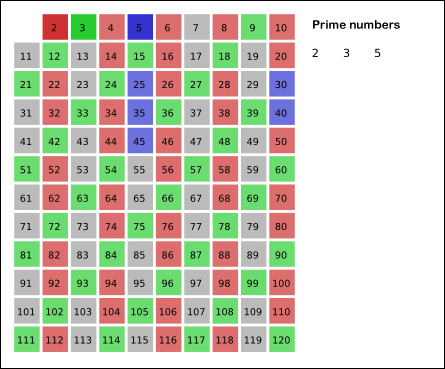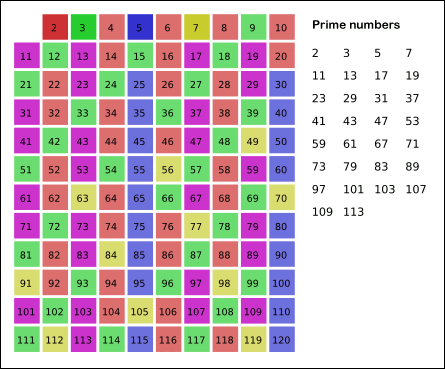
출처 : 위키백과
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기 수학에서 에라토스테네스의 체는 소수(소쑤)를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 알고리즘[편집] 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색) 자기 자신을 제외한 2의 배수를 모두 지운다. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초
ko.wikipedia.org
먼저 셀프 넘버에 해당하는 수를 구해내기 위해 boolean 배열 check를 만들었습니다.
그리고 나서, 1부터 10000까지 selfNum 함수를 반복하며 셀프넘버에 해당하지 않는 수는
check 배열에 true 처리하여 표시해주었습니다. ( 에라토스테네스의 체와 유사하게 )
모두 표시해준 이후 check 배열이 false인 숫자들만 출력해주었습니다.
함수 부분에 있는 문제이다 보니 이 문제를 풀이할 때 다른 것보다 중요한 것은
본인이 필요한 함수를 직접 정의해서 사용할 수 있는지를 묻는 것 같습니다.
함수 내부에서는 String temp에 수를 담은 뒤, 한 자리씩 떼어서 tmp 변수에 더해 셀프 넘버가 아닌 수들을 구해냈습니다.
또 이렇게 구해진 tmp가 10000보다 커질 경우 ArrayIndexOutOfBoundsException이 발생할 수 있으니
if문으로 체크해주는 거 꼭 확인하시기 바랍니다.
코드
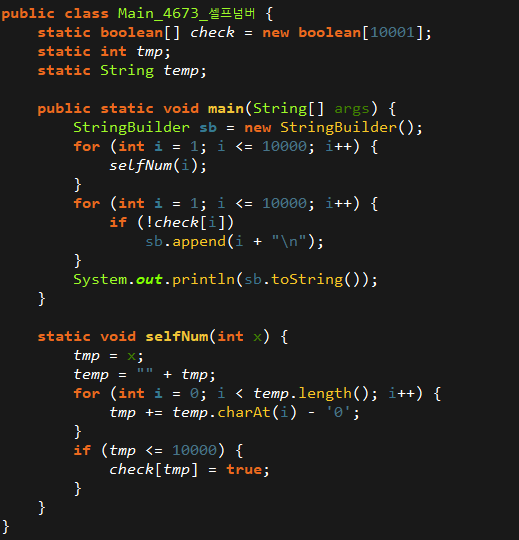
출처
https://www.acmicpc.net/problem/4673
4673번: 셀프 넘버
문제 셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다. 양의 정수 n이 주어졌을 때, 이 수를 시작해서 n, d(n), d(d(n)), d(d(d(n))), ...과 같은 무한 수열을 만들 수 있다. 예를 들어, 33으로 시작한다면 다음 수는 33 + 3 + 3 = 39이고, 그 다음 수는
www.acmicpc.net
'알고리즘 연습' 카테고리의 다른 글
| [ SWEA ] 1949. [모의 SW 역량테스트] 등산로 조성 JAVA 문제풀이 (0) | 2020.02.03 |
|---|---|
| [프로그래머스_2018 KAKAO BLIND RECRUITMENT] 1차_뉴스 클러스터링 (0) | 2020.02.02 |
| [백준_BOJ] 15596. 정수 N개의 합 _ JAVA (0) | 2020.01.03 |
| [ 삼성 SW 역량 테스트 A형 기출문제 ] 13458. 시험감독 _ JAVA 문제풀이 (0) | 2020.01.01 |
| [백준_BOJ] 2573. 빙산 _ JAVA (0) | 2019.12.31 |
 너구리의 코딩 블로그
너구리의 코딩 블로그